Метод деления пополам¶

Обзор¶

В математике метод деления пополам - это метод поиска корней, который применяется к любым непрерывным функциям, для которых известны два значения с противоположными знаками. Метод состоит из многократного деления пополам интервала, определяемого этими значениями, и последующего выбора подинтервала, в котором функция меняет знак и, следовательно, должна содержать корень. Это очень простой и надежный метод, но он также относительно медленный. Из-за этого его часто используют для получения грубого приближения к решению, которое затем используется в качестве отправной точки для более быстро сходящихся методов. Этот метод также называют методом деления интервала вдвое, методом двоичного поиска или методом дихотомии.

Метод¶

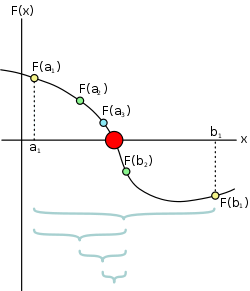
Метод применим для численного решения уравнения \(f(x) для действительной переменной :math:\),, где \(f\) - непрерывная функция, определенная на интервале \([a, b]\), а \(f(a)\) и \(f(b)\) имеют противоположные знаки. . В этом случае говорят, что \(a\) и \(b\) заключают в скобки корень, поскольку по теореме о промежуточном значении непрерывная функция \(f\) должна иметь хотя бы один корень в интервале \((a, b)\).

На каждом шаге метод делит интервал на две части, вычисляя среднюю точку \(c = \frac{a+b}{2}\) интервала и значение функции \(f(c)\) в этой точке. Если только c не является корнем (что очень маловероятно, но возможно), теперь есть только две возможности: либо \(f(a)\) и \(f(c)\) имеют противоположные знаки и скобки для корня, либо \(f(c)\) и \(f(b)\) иметь противоположные знаки и заключать в скобки корень. Метод выбирает подинтервал, который гарантированно является скобкой, в качестве нового интервала, который будет использоваться на следующем шаге. Таким образом, интервал, содержащий ноль \(f\), уменьшается по ширине на 50% на каждом шаге. Процесс продолжается до тех пор, пока интервал не станет достаточно малым.

Явно, если \(f(a)\) и \(f(c)\) имеют противоположные знаки, тогда метод устанавливает \(c\) как новое значение для \(b\), а если \(f(b)\) и \(f(c)\) имеют противоположные знаки, то метод устанавливает c как новое значение а. (Если \(f(c) = 0\), то c может быть принято как решение, и процесс останавливается.) В обоих случаях новые \(f(a)\) и \(f(b)\) имеют противоположные знаки, поэтому метод применим к этому меньшему интервалу .

Итерационные задачи¶

Вычислите \(c\), середину интервала, \(c=\frac{a+b}{2}\).
Вычислить значение функции в средней точке, \(f(c)\).
Если сходимость удовлетворительная (т. е. \(c-a\) достаточно мало или \(|f(c)|\) достаточно мало), верните c и прекратите повторение.
Изучите знак \(f(c)\) и замените \((a, f(a))\) или \((b, f(b))\) на \((c, f(c))\) так, чтобы в новом интервале было пересечение нуля.

Использование¶

Представьте, что мы хотим найти корень следующей функции:

\begin{equation} f(x) = \sin{(x)}, x \in [-1, 1] \end{equation}

Тогда код будет выглядеть так:

// example_root_bisection.cpp

#include <iostream>
#include "../src/numerary.hpp" // Numerary library

using namespace std;
using namespace numerary;

/* Function to found the root */
double f(double x) {
    return sin(x);
}

/* The main function */
int main() {

    const double eps = 1.e-9; // eps value for method (1.e-9 by default)
    double a = -1; // "a" value of segment [a, b]
    double b = 1; // "b" value of segment [a, b]
    double root;
    short int is_found;

    is_found = Numerary::root(f, a, b, &root, "bisection", eps);

    if (is_found == 1) {
        cout << "Root is in x = " << root << endl;
    } else {
        cout << "Method not allowed!" << endl;
    }

    return 0;
}