Интерполяция Лагранжа¶
Полином Лагранжа¶
В численном анализе полиномы Лагранжа используются для полиномиальной интерполяции. Для данного набора точек \((x_j, y_j)\), в котором нет двух одинаковых значений \(x_j\), многочлен Лагранжа является многочленом самой низкой степени, который принимает для каждого значения \(x_j\) соответствующее значение \(x_j\), так что функции совпадают в каждой точке.
Определение¶
Для набора из \(k+1\) точек данных \((x_0, y_0),\dots,(x_j, y_j),\dots,(x_k, y_k)\), где нет двух одинаковых \(x_j\), интерполяционный многочлен в форме Лагранжа представляет собой линейную комбинацию \(L(x):=\sum_{j=0}^{k} y_{j} \ell_{j}(x)\), базисных полиномов Лагранжа
где \(0 \leq j \leq k\). Обратите внимание на то, что при исходном предположении, что нет двух одинаковых \(x_j\), \(x_j - x_m \neq 0\), поэтому это выражение всегда хорошо определено. Причина, по которой пары \(x_i = x_j\) с \(y_i \neq y_j\) недопустимы, заключается в том, что не существует интерполяционной функции \(L\), такой что \(y_i=L(x_i)\); функция может получить только одно значение для каждого аргумента \(x_i\). С другой стороны, если также \(y_i = y_j\), то эти две точки фактически будут одной точкой.
Для всех \(i \neq j\), \(\ell(x)\) включает член \((x-x_i)\) в числителе, поэтому все произведение будет равно нулю при \(x = x_i\)
С другой стороны,
Другими словами, все базисные полиномы равны нулю при \(x = x_i\), за исключением \(\ell_i(x)\), для которого выполняется \(\ell_i(x_i) = 1\), поскольку в нем отсутствует член \((x - x_i)\).
Отсюда следует, что \(\ell_i(x_i) = y_i\), поэтому в каждой точке \(x_i\) \(L(x_i) = y_i + 0 + 0 + \dots + 0 = y_i\), показывая, что \(L\) точно интерполирует функцию.
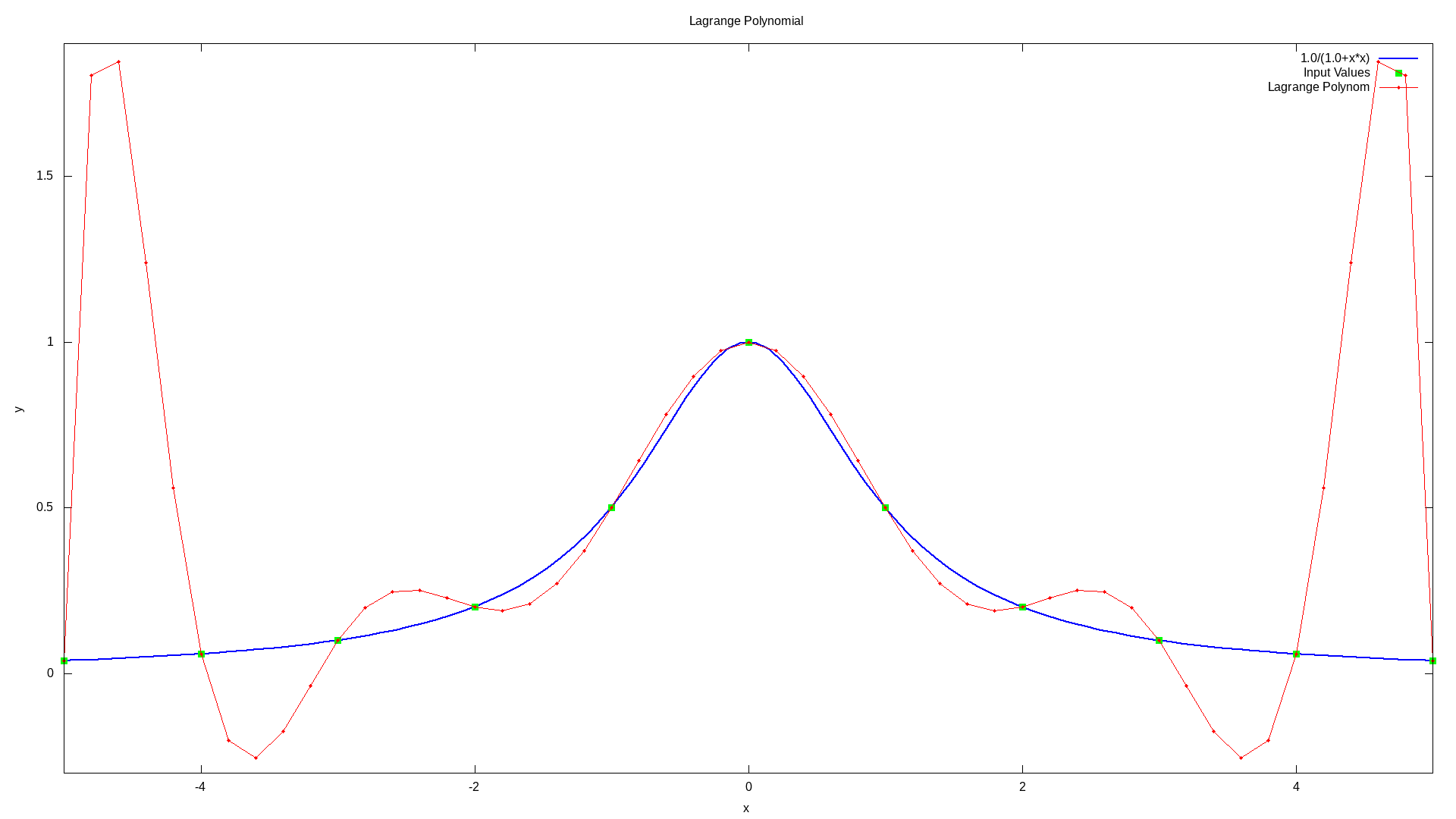
Пример Рунге¶
Функция \(f(x) = \frac{1}{1+x^2}\) не может быть точно интерполирована на \([−5, 5]\) с использованием многочлена десятой степени (пунктирная кривая) с равноотстоящими точками интерполяции. Этот пример, иллюстрирующий сложность, которую обычно можно ожидать от полиномиальной интерполяции высокой степени с равноотстоящими точками, известен как пример Рунге.
Использование¶
Представьте, что у нас есть следующие точки, и мы хотим построить многочлен Лагранжа из этих точек:
| X | Y |
|---|---|
| 2.0 | 10.0 |
| 3.0 | 15.0 |
| 5.0 | 25.0 |
| 8.0 | 40.0 |
| 12.0 | 60.0 |
Тогда код будет выглядеть так:
// example_lagrange_polynomial.cpp
#include <iostream>
#include "../src/numerary.hpp" // Numerary library
using namespace std;
using namespace numerary;
/* The main function */
int main() {
const int N = 5;
double *X = new double[N], *Y = new double[N];
double y, x;
// Points to interpolate
X[0] = 2.0; Y[0] = 10.0;
X[1] = 3.0; Y[1] = 15.0;
X[2] = 5.0; Y[2] = 25.0;
X[3] = 8.0; Y[3] = 40.0;
X[4] = 12.0; Y[4] = 60.0;
// Point where we want to get value of Lagrange Polynomial
x = 7.0;
y = Numerary::lagrange_polynomial(X, Y, x, N);
cout << "y(" << x << ") = " << y << endl;
delete[] X;
delete[] Y;
return 0;
}